# 数组
数组算法最重要的一点就是要明确每一个索引所代表的意义。
- 明确索引定义
- 二分查找
- 三路快排
- 快速排序
- 对撞指针
- 滑动窗口
# 明确索引定义
# Leetcode 283 Move Zeroes
https://leetcode-cn.com/problems/move-zeroes/
# 思路一:暴力法
- 新建一个相同大小的数组 temp,数组初始化的时候所有元素本身就默认为 0;
- 遍历原数组 nums,将不为 0 的元素依次放入 temp 中;
- 复制 temp 数组到 nums 数组;
class Solution {
public void moveZeroes(int[] nums) {
int[] temp = new int[nums.length];
int j = 0;
// 将不为 0 的移到 temp 的前面
for(int i = 0; i < nums.length; i++){
if (nums[i] != 0){
temp[j] = nums[i];
j++;
}
}
// 复制 temp 到 nums
for(int i = 0; i < nums.length; i++){
nums[i] = temp[i];
}
}
}
- 时间复杂度:代码中只有一层循环(虽然有2次循环,不过不是嵌套的),很明显是 O(n)。
- 空间复杂度:我们使用了一个临时数组,所以空间复杂度是 O(n)。
# 思路二:无需临时数组
仔细思考一下,其实这里辅助空间是完全没有必要的。
我们只需要在遇到非 0 元素的时候,直接把它赋值到前面就可以了。
而且由于非 0 元素的个数一定是小于或等于整个数组的元素个数的,所以在赋值到前面的时候,我们不用担心这个赋值会覆盖掉任何的数据。
整体思路如下:
- 遍历 nums,将非 0 元素复制到前面;
- 把后面的元素全部置为 0。
class Solution {
public void moveZeroes(int[] nums) {
// [0...j) 的元素非 0 元素
int j = 0;
for(int i = 0; i < nums.length; i++){
// 找到非 0 的元素
if (nums[i] != 0) {
// 将非 0 元素移动到前面
nums[j] = nums[i];
// 迭代索引
j++;
}
}
// [j...len-1] 全部置为 0
for(int i = j; i< nums.length; i++) {
nums[i] = 0;
}
}
}
# 思路三:一步到位
前面我们改进了空间复杂度。我们再看看代码的话会发现我们这里使用了 2 个步骤:复制非 0 元素和置 0 后面的元素。
一个改进思路就是:能不能在复制非0元素的同时将后面的元素置为 0。
要做到在复制非 0 元素的同时将后面的元素置为 0,很明显思路就是:将非 0 元素和 0 元素进行交换。
整体思路如下:
- 建立 2 个索引,一个是非 0 元素索引
j,一个是数组遍历索引i; - 遍历到数组第 i 个元素后,保证 [0…i] 中所有非 0 元素都按顺序排列在 [0…j) 当中,同时要保证 [j…i] 为 0
class Solution {
public void moveZeroes(int[] nums) {
// [0...j) 都是非 0 元素
int j = 0;
for(int i = 0; i < nums.length; i++) {
if(nums[i] != 0){
// 避免自身交换
if (i != j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
j++;
}
}
}
}
# Leetcode 27 Remove Elements
https://leetcode.cn/problems/remove-element/
本体其实就是 Leetcode 283 的变种,思路一致,这里不赘述直接给出代码。
func removeElement(nums []int, val int) int {
// 定义两个索引 i,j
// 保证 [0,j) 都不为 val,[j,i] 都为 val
j := 0
i := 0
for ; i < len(nums); i++ {
// 不断地将不为 val 的元素移动到 [0,j) 末尾
if nums[i] != val {
//避免自身交换
if i != j {
tmp := nums[i]
nums[i] = nums[j]
nums[j] = tmp
}
j++
}
}
return j
}
# Leetcode 26 Remove Duplicates From Sorted Array
https://leetcode.cn/problems/remove-duplicates-from-sorted-array/
本题由于数组是有序的,所以思路依旧可以参考 Leetcode283 和 Leetcode 27,建立两个索引,这次只需要保证 [0,j) 是有序不重复的,至于 [j,i] 的元素是什么值,就无所谓了。
func removeDuplicates(nums []int) int {
if len(nums) <= 1 {
return len(nums)
}
// 定义两个索引 i,j
// 保证 [0,j) 中每个元素都只出现一次,i 用来遍历数组
j := 1
for i := 1; i<len(nums); i++ {
// 不要和前一个元素重复
if nums[i] != nums[j - 1] {
// 避免自身交换
if i != j {
tmp := nums[i]
nums[i] = nums[j]
nums[j] = tmp
}
j ++
}
}
return j
// 模拟
// 1 2 3 3 3 4 5 5 6 7 8
// 1 2 3
// j
// i
// i
// 1 2 3 4 3 3 5 5 6 7 8
// j i
// 1 2 3 4 5 4 4 5 6 7 8
// j i
// i
}
# Leetcode 80 Remove Duplicates From Sorted Array II
https://leetcode.cn/problems/remove-duplicates-from-sorted-array-ii/
本体与 Leetcode 26 的区别在于:它允许重复两次,所以我们可以在 Leetcode 26 的基础上,加一个 flag 来标志是否重复过了,如果重复过了,就不许再重复了。
func removeDuplicates(nums []int) int {
// 定义两个索引 i,j
// 保证 [0,j) 中的元素最多重复两次,i 用来遍历 nums
i := 1
j := 1
// 用一个标记来标记 nums[j-1] 是否已经重复了
repeat := false
for ; i<len(nums); i++ {
// 不重复的,一直交换到 [0,j) 末尾
if nums[i] != nums[j-1] {
// 重置 repeat
repeat = false
// 避免自身交换
if i != j {
tmp := nums[i]
nums[i] = nums[j]
nums[j] = tmp
}
j++
} else {
// 重复的话,需要判断重复几次
if !repeat {
// 没重复过,允许重复一次,这时候做交换,
repeat = true
if i != j {
tmp := nums[i]
nums[i] = nums[j]
nums[j] = tmp
}
// 维护 [0,j) 都符合要求
j++
} else {
// 重复过了,就继续扫描
}
}
}
return j
}
# 二分查找
# 思想
- 有序数组
- 要查找的数为 target,取数组中间值 mid 跟 target 进行比较,来达到每次判断都能缩小一半的搜索范围,从而达到高效查询的目的:
- target == mid:直接返回
- target < mid:搜索 [...mid)
- target > mid:搜索 (mid...]
# 代码
# Java
package array_01;
/**
* @author Hedon Wang
* @create 2021-09-07 8:35 PM
*/
public class BinarySearch {
public static void main(String[] args) {
int[] arr = {1,2,3,4,7,9,11,34,67};
int target1 = 1;
int target2 = 11;
int target3 = 999;
System.out.println("target1 index: " + binarySearch(arr, target1));
System.out.println("target2 index: " + binarySearch(arr, target2));
System.out.println("target3 index: " + binarySearch(arr, target3));
}
/**
* 二分查找
*/
public static int binarySearch(int[] arr, int target){
return help(arr, 0, arr.length-1, target);
}
/**
* 二分查找辅助方法
*
* @param arr 待查询数组,必须是有序数组
* @param left 起始索引(包含)
* @param right 终止索引(包含)
* @param target 目标值
* @return target 所在 arr 的索引,不存在则返回 -1
*/
public static int help(int[] arr, int left, int right, int target){
// 递归终止条件
if (left > right) {
return -1;
}
// 中间索引:注意避免整型溢出
int midIndex = (right - left)/2 + left;
int mid = arr[midIndex];
// 缩小范围,递归查询
if(mid == target) {
// 等于直接返回
return midIndex;
} else if (target < mid){
// < 则找左边
return help(arr, left, midIndex-1, target);
} else {
// > 则找右边
return help(arr, midIndex + 1, right, target);
}
}
}
# Golang
package main
import "fmt"
func main() {
arr := []int{1, 2, 3, 4, 5, 7, 8, 9, 111, 3333, 22222}
target1 := 1
target2 := 111
target3 := 980
fmt.Println("target1 index:", binarySearch(arr, target1))
fmt.Println("target2 index:", binarySearch(arr, target2))
fmt.Println("target3 index:", binarySearch(arr, target3))
}
// binarySearch
// @Description 使用二分查找在一个有序数组 arr 中寻找 target 值所在的索引
// @param arr 待查询数组,有序
// @param target 目标值
// @return int 目标值所在数组的索引,找不到则返回 -1
func binarySearch(arr []int, target int) int {
return help(arr, 0, len(arr)-1, target)
}
// help
// @param arr 待查询数组,必须是有序数组
// @param left 起始索引(包含)
// @param right 终止索引(包含)
// @param target 目标值
// @return int target 所在 arr 的索引,不存在则返回 -1
func help(arr []int, left, right, target int) int {
// 递归退出条件
if left > right {
return -1
}
// 中建索引,注意避免整型溢出
midIndex := (right-left)/2 + left
mid := arr[midIndex]
// 缩小范围,递归查询
if target == mid {
// 等于直接返回
return midIndex
} else if target < mid {
// < 找左边
return help(arr, left, midIndex-1, target)
} else {
// > 找右边
return help(arr, midIndex+1, right, target)
}
}
# Leetcode 35 Search Insert Position
https://leetcode.cn/problems/search-insert-position/`
nums 有序且题目要求时间复杂度 O(logn),很明显是二分查找。
func searchInsert(nums []int, target int) int {
return help(nums, 0, len(nums)-1, target)
}
func help(nums []int, left, right, target int) int {
// 递归出口1:left 和 right 重合,只能做最后的尝试了
if left == right {
// 刚好是,或者 nums[left] 比 target 大,那就将 target 插在 left 的位置
if nums[left] >= target {
return left
} else {
// target 比 nums[left] 大,就插在 left 后面
return left+1
}
}
// 递归出口2:没找着,这里只有可能 left = 0,right = -1
if left > right {
return left
}
// 二分查找
midI := (left + right) / 2
if nums[midI] == target {
return midI
} else if nums[midI] > target {
return help(nums, left, midI-1, target)
} else {
return help(nums, midI+1, right, target)
}
}
# 三路快排
# 思想
三路快排,就是选定一个值,然后同时排序小于选定值,等于选定值,大于选定值这三种情况。
# Leetcode 75 Sort Colors
https://leetcode-cn.com/problems/sort-colors/
# 思路一:任意普通排序算法
- 任意普通排序算法都可以排成 000111222,但是效率较低。
# 思路二:计数排序
- 分别统计 0、1、2 元素的数量;
- 然后根据数量用 for 循环赋值即可。
# 思路二:三路快排
因为题目规定了数组的值只可能是 0、1 和 2,那么天然就可以用三路快排了。
- 选定 1 为选定值;
- 保证 [0...zero] 为 0,保证 [zero+1...i-1] 为 1,保证 [two....n-1] 为 2。
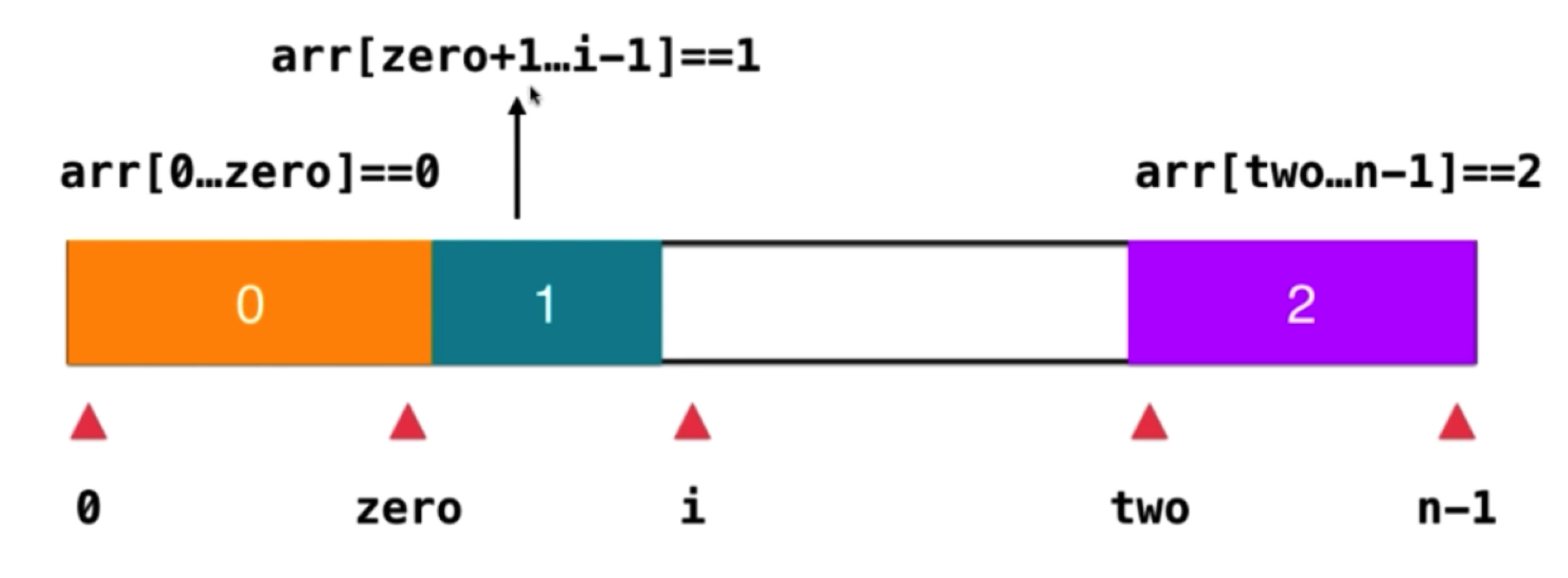
class Solution {
public void sortColors(int[] nums) {
// 保证 [0...zero] 为 0
// 保证 [zero+1...i-1] 为 1
// 保证 [two....n-1] 为 2
int zero = -1;
int two = nums.length;
for(int i=0; i<two;) {
// 保证 [zero+1...i-1] 为 1
if(nums[i] == 1) {
i ++;
continue;
}
// 将 nums[i] 和 nums[zero+1] 进行交换,并且递增 zero
// 保证 [0...zero] 为 0 和 保证 [zero+1...i-1] 为 1
if(nums[i] == 0) {
int temp = nums[i];
nums[i] = nums[zero+1];
nums[zero+1] = temp;
zero ++;
i ++;
continue;
}
// 将 nums[i] 和 nums[two-1] 进行交换,并且递减 two
// 保证 [two....n-1] 为 2
if (nums[i] == 2){
int temp = nums[i];
nums[i] = nums[two-1];
nums[two-1] = temp;
two --;
}
}
}
}
# 快速排序
# 思想
选定一个基准 pivot,然后将比 pivot 大的移到它后面,比 pivot 小的移到它前面,然后再对两边进行递归快排,直接排序完成。
# 算法
# Java
public class QuickSort {
public static void main(String[] args) {
int[] arr1 = {0, 4, 11, -22, 3, 8, 232};
quickSort(arr1);
printArr(arr1);
int[] arr2 = {0,1};
quickSort(arr2);
printArr(arr2);
int[] arr3 = {};
quickSort(arr3);
printArr(arr3);
int[] arr4 = {1, -1};
quickSort(arr4);
printArr(arr4);
}
public static void quickSort(int[] arr) {
help(arr, 0, arr.length -1);
}
/**
* 对 arr[left...right] 进行快速排序
*/
public static void help(int[] arr, int left, int right) {
// 递归出口
if (left >= right) {
return;
}
int start = left;
int end = right;
// 取出标准值
int pivotIndex = start;
int pivot = arr[pivotIndex];
// 快排
while (start < end) {
// 先从右往左
while (arr[end] >= pivot && end > start) {
end --;
}
// 退出循环,如果还没遍历完,说明找到比 pivot 小的,交换
if (end > start) {
arr[pivotIndex] = arr[end];
pivotIndex = end;
}
// 再从左往右
while (arr[start] <= pivot && start < end) {
start ++;
}
// 退出循环,如果还没遍历完,说明找到比 pivot 大的,交换
if (start < end) {
arr[pivotIndex] = arr[start];
pivotIndex = start;
}
}
// 复位
arr[pivotIndex] = pivot;
// 分别对左右两边进行快排
help(arr, left, pivotIndex-1);
help(arr, pivotIndex + 1, right);
}
/**
* 打印
*/
public static void printArr(int[] arr){
String s = "";
for (int i = 0; i < arr.length; i++) {
s += arr[i] + " ";
}
System.out.println(s);
}
}
# Golang
package main
import (
"fmt"
"strconv"
)
func main() {
arr1 := []int{0, 4, 11, -22, 3, 8, 232}
quickSort(arr1)
printArr(arr1)
arr2 := []int{0, 1}
quickSort(arr2)
printArr(arr2)
arr3 := make([]int, 0)
quickSort(arr3)
printArr(arr3)
arr4 := []int{1, 2}
quickSort(arr4)
printArr(arr4)
}
/**
* 快排
*/
func quickSort(arr []int) {
help(arr, 0, len(arr)-1)
}
/**
* 对 arr[left...right] 进行快排
*/
func help(arr []int, left, right int) {
// 递归出口
if left >= right {
return
}
start := left
end := right
// 基准
pivotIndex := start
pivot := arr[pivotIndex]
// 快排
for end > start {
// 先从右往左,找小的
for end > start && arr[end] >= pivot {
end--
}
// 退出循环,如果还没遍历完,说明找到比 pivot 小的,交换
if end > start {
arr[pivotIndex] = arr[end]
pivotIndex = end
}
// 再从左往右,找大的
for start < end && arr[start] <= pivot {
start++
}
// 退出循环,如果还没遍历完,说明找到比 pivot 大的,交换
if start < end {
arr[pivotIndex] = arr[start]
pivotIndex = start
}
}
// 复位
arr[pivotIndex] = pivot
// 对左右两边分别进行快排
help(arr, left, pivotIndex-1)
help(arr, pivotIndex+1, right)
}
// 打印
func printArr(arr []int) {
s := ""
for i := 0; i < len(arr); i++ {
s += strconv.Itoa(arr[i]) + " "
}
fmt.Println(s)
}
# Leetcode 215 Kth Largest Element in an Array
https://leetcode-cn.com/problems/kth-largest-element-in-an-array/
# 思路一:优先队列
- 建立一个含有 k 个元素的优先级队列,Java 中优先级队列默认是小顶堆,也就是队首的值是最小的;
- 遍历 nums,如果队列不满,则元素加入队列;
- 如果队列已满,则比较 nums 与队首数的大小,如果大于队首,则队首出队,新元素入队;
- 遍历完 nums,队首就是第 k 大的元素。
class Solution {
public int findKthLargest(int[] nums, int k) {
// 这个小顶堆的实现,默认就是了,可以不写
// 写这个是为了方便灵活,如果需要用大顶堆的话,就改成 o2-o1 即可
PriorityQueue<Integer> queue = new PriorityQueue<>(k, new Comparator<Integer>(){
@Override
public int compare(Integer o1, Integer o2) {
return o1 - o2;
}
});
for(int i=0; i<nums.length; i++){
if(i < k) {
// 队列未满,直接进队
queue.add(nums[i]);
} else {
int head = queue.peek();
// 队列已满,比较队首与 nums[i] 的大小,如果 nums[i] 大,则顶替队首进队
if( head < nums[i]) {
queue.poll();
queue.add(nums[i]);
}
}
}
// 由于优先级队列自动排序,所以队首就是第 k 大的数了
return queue.peek();
}
}
# 思路二:快速排序
- 取基准值,进行一遍快排;
- 判断基准值所在的位置,如果基准值刚好在第 k 大的位置上,直接返回基准值;
- 否则,就根据基准值的位置确定在左边寻找还是在右边寻找;
- 然后根据 k 值,重新确定需要在左边或者右边寻找第 k` 大的值;
- 直至找到。
class Solution {
public int findKthLargest(int[] nums, int k) {
return help(nums, 0, nums.length-1, k);
}
/**
* @param nums 待查询数组
* @param left 左边界
* @param right 有边界
* @param k 范围内的第 k 大
*/
public int help(int[] nums, int left, int right, int k) {
// 递归出口
if (left > right) {
return -1;
}
if (left == right && k == 1) {
return nums[left];
}
int start = left;
int end = right;
// 基准值
int pivotIndex = start;
int pivot = nums[start];
// 目标索引
int targetIndex = right - k + 1;
// 快排
while(start < end) {
// 先从右往左,找小于 pivot 的值
while( end > start && nums[end] >= pivot) {
end--;
}
// 跳出循环,如果还没遍历完,说明找到比 pivot 小的,交换
if( end > start) {
nums[pivotIndex] = nums[end];
pivotIndex = end;
}
// 再从左往右找,找大于 pivot 的值
while( start < end && nums[start] <= pivot) {
start++;
}
// 跳出循环,如果还没遍历完,说明找到比 pivot 大的,交换
if( start < end) {
nums[pivotIndex] = nums[start];
pivotIndex = start;
}
}
// 判断 pivot 的位置
if (pivotIndex == targetIndex) {
// 刚好在目标索引上,那就直接返回 pivot
return pivot;
} else if(pivotIndex < targetIndex) {
// 比目标索引小,那就说明应该在右边找,重新确定边界进行快排
int newLeft = pivotIndex + 1;
int newRight = right;
k = k;
return help(nums, newLeft, newRight, k);
} else {
// 比目标索引大,那就说明应该在左边找,重新确定边界进行快排
int newLeft = left;
int newRight = pivotIndex - 1;
int rightCount = right - pivotIndex + 1;
// 因为右边的都比较大,所以新的第 k 大应该减去右边的个数
k = k - rightCount;
return help(nums, newLeft, newRight, k);
}
}
}
# 对撞指针
# Leetcode 167 Two Sum II Input Array Is Sorted
https://leetcode-cn.com/problems/two-sum-ii-input-array-is-sorted/
# 思路一:对撞指针
- 因为 nums 天然有序,所以可以采取左右夹击的方式;
- nums[left] + nums[right],与 target 进行比较
- 如果等于 target,直接返回;
- 如果小于 target,则左边前进,增大值;
- 如果大于 target,则右边后退,减小值;
class Solution {
public int[] twoSum(int[] numbers, int target) {
int left = 0;
int right = numbers.length-1;
// 左右夹击
while (left < right ){
// 等于 target,直接返回,注意题目要求下表从 1 开始
if(numbers[left] + numbers[right] == target) {
return new int[]{left + 1, right + 1};
} else if(numbers[left] + numbers[right] < target) {
// 小于 target,则左边前进,增大值
left ++;
} else {
// 大于 target,则右边后退,减小值
right--;
}
}
return null;
}
}
# Leetcode 125 Valid Palindrome
https://leetcode-cn.com/problems/valid-palindrome/
# 思路一:对撞指针
- 判断是否回文,很明显可以用对撞指针的方式;
- 需要注意两点:
- 只考虑数字和字母;
- 不考虑大小写
class Solution {
public boolean isPalindrome(String s) {
if(s == null || s.length() == 0){
return true;
}
int left = 0;
int right = s.length()-1;
while(left < right){
while(left < s.length() && !charIsCharacterOrNumber(s.charAt(left))){
left++;
}
while( right >= 0 && !charIsCharacterOrNumber(s.charAt(right))){
right--;
}
if(left >= right){
break;
}
if(left < right && !charIsSameIgnoreCase(s.charAt(left), s.charAt(right))){
return false;
}
left++;
right--;
}
return true;
}
// 只考虑数字和字母
public boolean charIsCharacterOrNumber(char c){
return (c >= 48 && c<=57) || (c>=65 && c<=90) || (c>=97 && c<=122);
}
// 忽略大小写
public boolean charIsSameIgnoreCase(char c1, char c2){
return c1 == c2 || (c1 >= 65 && c2>=65 && Math.abs(c1-c2) == 32);
}
}
# Leetcode 345 Reverse Vowels Of A String
https://leetcode-cn.com/problems/reverse-vowels-of-a-string
# 思路一:对撞指针
- 因为题目只要反转元音字母,所以我们需要定义一个方法来判断当前字符是否是元音字母;
- 采用对撞指针的方式,分别找到左边的原因和右边的元音,进行交换;
- 然后左右两个指针再向中间靠拢,继续尝试交换元音字母;
class Solution {
public String reverseVowels(String s) {
if ( s == null || s.length() <= 1) {
return s;
}
int left = 0;
int right = s.length() - 1;
char[] arr = s.toCharArray();
while(left < right) {
// 找到左边的元音字母
while(left < right && !isVowel(arr[left])) {
left ++;
}
// 找到右边的元音字母
while( right > left && !isVowel(arr[right])) {
right --;
}
// 二者交换位置
if ( left < right ) {
char temp = arr[left];
arr[left] = arr[right];
arr[right] = temp;
}
// 继续向中间靠拢
left ++;
right --;
}
return new String(arr);
}
public boolean isVowel(char c) {
return c == 'a' || c == 'e' || c == 'i' || c == 'o' || c == 'u'
|| c == 'A' || c == 'E' || c == 'I' || c == 'O' || c == 'U';
}
}
# Leetcode 11 Container With Most Water
https://leetcode-cn.com/problems/container-with-most-water/
# 思路一:对撞指针
本题的核心在于确定一个 s = (x2-x1)*Min(y1,y2) 的最大值;
建立两个指针,一个在头一个在尾,这个时候,(x2-x1)是最大的,我们要尝试找到更大的 s,找的过程中(x2-x1)只能变小,那么就只能尽可能找到更大的 Min(y1,y2),这个时候:
- 移动 Max(y1,y2)? 不可以,因为移动 y` = Max(y1,y2),无论 y` 怎么变,都不可能大于 Min(y1,y2),所以不可能使得 s 变大;
- 故而只能移动 Min(y1,y2),这样可以尝试找到更大的 s;
以此下去,在 y1 和 y2 不断靠近的过程中,一直只移动 Min(y1,y2),尝试找到更大的 s
func maxArea(height []int) int {
x1 := 0
x2 := len(height) - 1
y1 := height[x1]
y2 := height[x2]
s := (x2 - x1) * int(math.Min(float64(y1), float64(y2)))
for ; x1 < x2; {
// 尝试移动小的 y 对应的 x,找到更大的 s
if y1 < y2 {
// y1 小,就移动 x1,在 y1 大于 y2 之前尝试找到更大的 s,
for ; x1 < x2 && y1 < y2; {
x1 ++
y1 = height[x1]
new_s := (x2 - x1) * int(math.Min(float64(y1), float64(y2)))
if new_s > s {
s = new_s
break
}
}
} else {
// y2 小,就移动 x2,在 y2 大于 y1 之前尝试找到更大的 s,
for ; x1 < x2 && y2 <= y1; {
x2 --
y2 = height[x2]
new_s := (x2 - x1) * int(math.Min(float64(y1), float64(y2)))
if new_s > s {
s = new_s
break
}
}
}
}
return s
}
# 滑动窗口
# 思想
所谓滑动窗口,就是在数组中建立两个索引,这两个索引围成一个窗口,然后通过修改索引来滑动窗口并找到问题的解。
# Leetcode 209 Minimum Size Subarray Sum
https://leetcode-cn.com/problems/minimum-size-subarray-sum/
# 思路一:滑动窗口
- 建立一个窗口 [left...right],从 [0...0] 开始;
- 先滑动右窗口,直到满足条件,即 sum >= target;
- 因为题目要小的,所以再滑动左窗口,缩小窗口,直到刚好不满足条件,那么在不满足条件之前就是本次滑动获得的满足条件的最小窗口,记下来;
- 继续往前滑动窗口,看看有没有更小的窗口,记录更小的窗口;
- 直到遍历完整个数组。
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int sum = 0;
int result = 0;
// 左窗口
int left = 0;
// 右窗口
int right = 0;
// 滑动窗口
while(left <= right && right < nums.length) {
// 滑动右窗口,增大 sum,直到满足条件
while(sum < target && right < nums.length){
sum += nums[right];
right ++;
}
// 判断是否满足条件,不满足条件,说明已经滑动到头了,没必要再尝试了
if (sum < target) {
break;
}
// 滑动左窗口,减小 sum,直到不满足条件
while (sum >= target && left < right) {
sum -= nums[left];
left ++;
}
// 记下最后一个满足条件的窗口
if(result != 0) {
result = result >= (right-left+1)?(right-left+1):result;
} else {
result = right - left + 1;
}
}
return result;
}
}
# Leetcode 3 Longest Substring Without Repeating Characters
https://leetcode-cn.com/problems/longest-substring-without-repeating-characters/
# 思路一:滑动窗口
因为题目要求寻找最长不重复子串的长度,而且 s 由英文字母、数字、符号和空格组成,也就是由 ASCII 组成。很显然一个子串,就构成了一个窗口,那我们在滑动窗口的时候,就需要做一些记录,来判断子串中的字符是否重复了。ASCII 只有 128 个,所以我们可以利用一个 128 位的数组,来辅助我们记录当前窗口所包含的字符的出现情况,从而辅助窗口的滑动,解决问题。
- 建立一个 int[128] 数组来记录字符出现情况;
- 建立一个窗口 [left...right),其含义表示 [left...right) 是不重复的子串;
- 从右开始滑动窗口,如果还没重复,且还没遍历完字符串,就一直往右;
- 向右停止的时候,跟当前已经含有的 result 进行比较,记录大的;
- 向右停止的时候,如果还没遍历完,那就是遇到重复的了,从左开始删除字符,直到找到那个重复的;
- 右窗口继续往右,继续重试,直到遍历完;
class Solution {
public int lengthOfLongestSubstring(String s) {
if ( s == null || s.length() == 0){
return 0;
}
if (s.length() == 1) {
return 1;
}
// 记录字符的出现情况
int[] has = new int[128];
// 确保 [left...right) 是不含有重复字符的子串
int left = 0;
int right = 1;
has[s.charAt(left)] = 1;
// 结果
int result = 0;
// 滑动窗口
while(left < right && right < s.length()) {
// 先向右扩容
while(right < s.length() && has[s.charAt(right)] == 0){
has[s.charAt(right)] = 1;
right ++;
}
// 记下当前最长长度
result = (right - left) > result ? (right - left) : result;
// 走到头了,直接结束循环
if (right == s.length()) {
break;
}
// 右窗口没走到头,说明遇到重复的字符了,也就是 s.charAt(right) 重复了
// 从左边找到第一个 s.charAt(right),并截掉它及前面的部分
// 让窗口可以继续往右移动,尝试寻找更长的子串
while(s.charAt(left) != s.charAt(right) && left < right) {
has[s.charAt(left)] = 0;
left ++;
}
// 截掉
if (right < s.length() && left < right) {
has[s.charAt(left)] = 0;
left ++;
// 右边的现在不会跟之前的重复了,加上
has[s.charAt(right)] = 1;
right ++;
}
}
return result;
}
}
# Leetcode 438 Find All Anagrams In A String
https://leetcode-cn.com/problems/find-all-anagrams-in-a-string/
# 其他好题
# Leetcode 88 Merge Sorted Array
https://leetcode-cn.com/problems/merge-sorted-array/
# 思路一:反向操作
因为题目希望设计一个复杂度为 O(m + n) 的算法,那就意味着只能遍历一遍 nums1 和 nums2。因为 nums1 后面都是 0,所以我们可以反向操作,从后面开始插入 nums1,这样插入到前面的时候,就只遍历一遍 nums1 和 nums2 了,而且也排好序了。
- 建立一个索引 done,表示 [done...m+n) 已经排好序了;
- 从后比较 nums1 和 nums2,谁大就放到 nums1[done],然后 done--;
- 一直比较,比较到其中一个数组个数为 0:
- 如果是 nums2 比完了,天然结束;
- 如果是 nums1 比完了,那就把 nums2 剩下的元素放到 nums1 前面。
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
// 保证 num1[done...m+n) 是排好序的
int done = m + n;
// 从后比较
while(n > 0 && m > 0) {
// 选大的放后面,然后 done 往前推
if ( nums1[m-1] >= nums2[n-1]) {
nums1[--done] = nums1[--m];
} else {
nums1[--done] = nums2[--n];
}
}
// nums2 还没比较完,则全部移动到 nums1 的前面
if ( n > 0 ) {
for (int i=0; i < n; i++){
nums1[i] = nums2[i];
}
}
}
}
