# 回溯法
回溯三部曲:
确定回溯函数的返回值和参数
回溯算法中函数的返回值一般为 void,一般将结果保存在一个全局变量中;
因为回溯算法需要的参数并不像二叉树的递归过程那么容易一次性确定下来,所以一般是先写逻辑,然后需要什么参数,就填什么参数;
void backtracking(参数,已选择的列表)确定回溯终止条件
既然是树形结构,那么遍历树形结构就一定要有终止条件,所以回溯也有要终止条件。
什么时候达到了终止条件?从树中就可以看出,一般来说搜索到叶子节点了,也就找到了满足条件的一个答案,把这个答案存放起来,并结束本层递归。
if (终止条件) { 将已选择的列表存放在结果中; return; }确定回溯搜索的遍历过程
回溯法一般是在集合中递归搜索,集合的大小构成了树的宽度,递归的深度构成了树的深度,如下图所示。
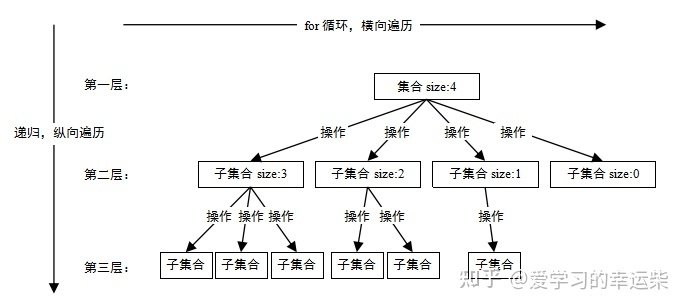
for (确定起点,选择:本层集合中的元素(树中节点孩子的数量就是集合的大小)) { 处理节点; backtracing(路径,已选择列表); 回溯,撤销处理结果; }
# 树形问题
# Leetcode 17 Letter Combinations Of A Phone Number
https://leetcode.cn/problems/letter-combinations-of-a-phone-number/
因为题目要求映射关系要一一对应,本题是典型的树形问题,所以我们只需要尝试前面字母的每一种情况,然后再尝试下一个,直到遍历完 digits。
digits 是数字字符串
s(digits) 是 digits 所能代表的字母字符串
s(digits[0...n-1])
= letter(digits[0]) + s(digits[1...n-1])
= letter(digits[0]) + letter(digits[1]) + s(digits[2...n-1])
= ...
var m map[int][]byte
func letterCombinations(digits string) []string {
if digits == "" {
return nil
}
// 用 map 来记录每一个映射关系
m = make(map[int][]byte, 8)
m[2] = []byte{'a', 'b', 'c'}
m[3] = []byte{'d', 'e', 'f'}
m[4] = []byte{'g', 'h', 'i'}
m[5] = []byte{'j', 'k', 'l'}
m[6] = []byte{'m', 'n', 'o'}
m[7] = []byte{'p', 'q', 'r', 's'}
m[8] = []byte{'t', 'u', 'v'}
m[9] = []byte{'w', 'x', 'y', 'z'}
return help(digits, 0, len(digits), "")
}
// DFS
// index: 当前尝试的数字
func help(digits string, index, end int, s string) []string {
if index == end {
return nil
}
var res []string
// 取出当前数字可以代表的字母
cs := m[int(digits[index] - '0')]
// 尝试每一种情况,并继续尝试下一个数字
for i:=0; i<len(cs);i++ {
res = append(res, help(digits, index+1, end , s + string(cs[i]))...)
}
return res
}
# Leetcode 93 Restore IP Address
https://leetcode.cn/problems/restore-ip-addresses/
本题跟 Leetcode 17 其实是同一类问题,只是在不断往下尝试的时候,该尝试是有限制的:
- 每确定一个整数,最多尝试 3 位数;
- 整数一定要 0~255,且不能有前导零;
- s 一定要够划分为 4 个部分;
所以整体思路:
- 逐渐确定 4 个整数;
- 每一个整数尝试 3 次,分别为长度 1,长度 2 和长度 3;
- 如果整数合法,就递归尝试下一个整数;
- 直到尝试第 4 个整数,如果还满足条件,就存入 res,如果不满足,就丢弃;
// 答案
var res []string
func restoreIpAddresses(s string) []string {
// 重置 res
res = make([]string, 0)
if len(s) < 4 {
return nil
}
help(s, 0, 1, 4, "")
return res
}
// s: 原ip字符串
// index: 即将要遍历 s 的下标
// wantCount:即将要确定第几个整数
// totalCount: 需要确定多少个整数,固定为 4
// ip: 目前已经构造好的 ip 地址
func help(s string, index, wantCount, totalCount int, ip string) {
// 递归出口:确定最后一个整数
if wantCount == totalCount {
// s 必须用完
tmp := s[index:]
if validate(tmp) {
res = append(res, ip + "." + tmp)
}
return
}
// DFS,每个整数最多尝试3位
for i:=index; i < index + 3 && i <len(s);i++ {
num := s[index:i+1]
if !validate(num) {
continue
}
newIp := ip
if wantCount == 1 {
newIp = num
} else {
newIp = ip + "." + num
}
// 继续尝试下一位
help(s, i+1, wantCount+1,totalCount, newIp)
}
}
// 0 ~ 255
func validate(s string) bool {
// 长度不可能超过3,不可能小于1
if len(s) > 3 || len(s) < 1{
return false
}
// 不能含有前导零
if len(s) > 1 && s[0] == '0' {
return false
}
i, _ := strconv.Atoi(s)
return i >= 0 && i <= 255
}
# Leetcode 131 Palindrome Partitioning
https://leetcode.cn/problems/palindrome-partitioning/
本题思路还是跟前两题一致,只不过尝试的时候判断条件变成了 palindrome,本题还可以再引入 map 来减少重复计算。
// 0: 未确定
// 1: 确定回文
// 2: 确定不回文
var m map[string]int
func partition(s string) [][]string {
m = make(map[string]int)
var tmp []string
return help(s, 0, tmp)
}
// s: 原字符串
// startIndex: 要开始尝试寻找回文串的下标
// tmp: 当前已经确定的回文串
func help(s string, startIndex int, tmp []string) [][]string {
var res [][]string
// 递归出口1:s 为 空
if len(s) == 0 {
return nil
}
// 递归出口2:扫描完 s 了
if startIndex == len(s) {
tmp1 := make([]string, len(tmp))
copy(tmp1, tmp) // 这里需要 copy,否则后面涉及到 tmp 扩容的话,指针操作会影响到 tmp 的值
res = append(res, tmp1)
return res
}
for i := startIndex + 1; i <= len(s); i++ {
si := s[startIndex:i]
if palindrome(si) {
res = append(res, help(s, i, append(tmp, si))...)
}
}
return res
}
// 判断 s 是否回文
// 引入 map 来减少重复计算
func palindrome(s string) bool {
if m[s] == 1 {
return true
}
if m[s] == 2 {
return false
}
left := 0
right := len(s) - 1
for left < right {
if s[left] != s[right] {
m[s] = 2
return false
}
left++
right--
}
m[s] = 1
return true
}
# 排列问题
排列问题,经常可以加一个 visited[] 来记录访问情况。
# Leetcode 46 Permutations
https://leetcode.cn/problems/permutations/
根据题目意思,nums 里的数字,每个只能用一次。
例如:我们用了 [1],就只剩下 [2,3],再用 [2],就只剩下 [3]。
所以我们可以设置一个全局变量 visited,来记录哪些数字是访问了的,这样就不会重复访问数字了。
即 Perms( nums[0...n-1] ) = { 取出一个数字 } + Perms( nums[{0...n-1} - 这个数字] )
递归体思路如下:
- 访问没有访问过的数字;
- 加入该数字,设置 visited 访问标志,然后递归尝试其他数字;
- 当所有数字都已经尝试完了,就输出一个结果;
- 递归返回后,重置 visited,然后移除刚刚尝试的数字,继续回溯以不同顺序尝试其他情况;
var visited []bool
var res [][]int
func permute(nums []int) [][]int {
visited = make([]bool, len(nums))
res = make([][]int, 0)
var tmp []int
help(nums, tmp)
return res
}
// tmp: 保存当前已经尝试了的数字
func help(nums, tmp []int) {
// 递归出口1:空数组
if len(nums) == 0 {
return
}
// 递归出口2:tmp 长度跟 nums 一样
if len(tmp) == len(nums) {
tmp1 := make([]int, len(tmp))
copy(tmp1, tmp)
res = append(res, tmp1)
return
}
// 递归体:不断尝试没有访问过的数字
for i := 0; i < len(nums); i++ {
// 只访问没有访问过的数字
if !visited[i] {
// 1. 设置访问标记
visited[i] = true
tmp = append(tmp, nums[i])
// 2. 递归尝试
help(nums, tmp)
// 3. 还原,继续回溯尝试
visited[i] = false
tmp = tmp[:len(tmp)-1]
}
}
return
}
# Leetcode 47 Permutations ii
https://leetcode.cn/problems/permutations-ii/
/*
分析如下:
[1,1,2]
1/ 1|(之前有1了,去重) \2
[1,2] [1,2] [1,1]
1/ \2 1/ \1 (之前有1了,去重)
[2] [1] [1]
2↓ 1↓ 1↓
112 121 211
总结:
在堆回溯产生的多个树中,每个树进行层次遍历的时候,
每一层,不尝试 `相同的数字`,因为结果必然是相同的。
*/
class Solution {
// 总结果
List<List<Integer>> res = new ArrayList<>();
// 存放剩下的数字
LinkedList<Integer> numsList = new LinkedList<>();
// 一种结果
LinkedList<Integer> oneRes = new LinkedList<>();
public List<List<Integer>> permuteUnique(int[] nums) {
if(nums == null || nums.length == 0){
return res;
}
for(int num: nums){
numsList.add(num);
}
dfs(nums);
return res;
}
public void dfs(int[] nums){
//一种结果里面如果元素 = nums.length,说明已经满足条件了
if(oneRes.size() == nums.length){
res.add((LinkedList<Integer>)oneRes.clone());
return;
}
//每一层去重
HashSet<Integer> set = new HashSet<>();
//尝试当前层剩下的情况
for(int i=0;i<numsList.size();i++){
int num = numsList.get(i);
//去重
if(!set.contains(num)){
set.add(num);
oneRes.add(num);
numsList.remove(i);
//递归
dfs(nums);
//回溯
oneRes.removeLast();
numsList.add(i,num);
}
}
}
}
# 组合问题
# Leetcode 77 Combinations
https://leetcode.cn/problems/combinations/
组合问题,不在乎顺序,只要每个组合是不同的就可以了。
本题手写一下分析过程后,思路就很明确了:

var res [][]int
func combine(n int, k int) [][]int {
res = make([][]int, 0)
var tmp []int
help(n,k,1,tmp)
return res
}
// n: 题目中的 n,即可取整数的范围
// k: 要多少个数组合
// start: 开始尝试的数
// tmp: 当前组合
func help(n, k, start int, tmp []int) {
// 递归出口:已经满足个数了
if len(tmp) == k {
tmp1 := make([]int, len(tmp))
copy(tmp1, tmp)
res = append(res, tmp1)
return
}
// 继续尝试
for i:=start;i<=n;i++ {
// 加入当前值
tmp = append(tmp, i);
// 尝试下一个值
help(n, k, i+1, tmp)
// 回溯,继续尝试
tmp = tmp[:len(tmp)-1]
}
}
# Leetcode 39 Combination Sum
https://leetcode.cn/problems/combination-sum/submissions/
本题也是经典的使用回溯来解决组合问题。我们先来关注题要点:
- 无重复的 candidates 中寻找数字,让 sum = target
- 数字可以重复使用
递归出口比较好定义,关键是递归体的参数确定,我们定义 start 来遍历 candidates,start 指明本轮回溯的起始点。
由于数字可以重复使用,所以尝试完当前数字后,start 不需要 + 1,即下面的 help(candidates, i, target-n, tmp)。
又为了避免重复,所以 newStart >= oldStart,不走回头路,即 for i:=start; i< len(candidates);i++。
具体实现如下:
var res [][]int
func combinationSum(candidates []int, target int) [][]int {
res = make([][]int, 0)
var tmp []int
help(candidates, 0, target, tmp)
return res
}
// start: 开始尝试的下标
func help(candidates []int, start, target int, tmp[]int) {
// 递归出口1:没找到
if target < 0 {
return
}
// 递归出口2:找到
if target == 0 && len(tmp) != 0 {
tmp1 := make([]int, len(tmp))
copy(tmp1, tmp)
res = append(res, tmp1)
return
}
// 继续从 start 开始尝试
for i:=start; i< len(candidates);i++ {
n := candidates[i]
// 1. 加入当前数
tmp = append(tmp, n)
// 当前的 n 还可以再重试
// 但是不回头,也就是 newStart >= oldStart,避免重复
// 2. 尝试
help(candidates, i, target-n, tmp)
// 3. 回溯,试下一个
tmp = tmp[:len(tmp)-1]
}
}
# Leetcode 40 Combination Sum II
https://leetcode.cn/problems/combination-sum-ii/
本题相比 39 其实更好确定递归参数,本题要求数字不能重复使用(但是相等的数字在不同的位置的话,可以使用),所以在上题的基础上,newStart = oldStart+1 即可。
但是题目给的 candidates 是乱序且有可能重复的,所以我们有两种思路:
- 然后在每一层遍历的时候加一个 map 来去重,参考 Leetcode 47 Permutations ii,思路很类似,效率较低;
- 先对 candidates 进行排序,然后在尝试的时候,如果后一个跟前一个相同,就不尝试后一个,这样就不会重复了,效率较高。
var res [][]int
func combinationSum2(candidates []int, target int) [][]int {
res = make([][]int, 0)
var tmp []int
// 排序
sort.Ints(candidates)
help(candidates, 0, target, tmp)
return res
}
// start: 开始尝试的 candidates 的下标
func help(candidates []int, start, target int, tmp []int) {
// 递归出口1:没找到
if target < 0 {
return
}
// 递归出口2:找到
if target == 0 && len(tmp) != 0 {
tmp1 := make([]int, len(tmp))
copy(tmp1, tmp)
res = append(res, tmp1)
return
}
for i:=start; i<len(candidates); i++{
// 去重
if i > start && candidates[i] == candidates[i-1] {
continue
}
n := candidates[i]
// 1. 加入当前数字
tmp = append(tmp, n)
// 2. 尝试
help(candidates, i+1, target-n, tmp)
// 3. 回溯
tmp = tmp[:len(tmp)-1]
}
}
# Leetcode Combination Sum III
https://leetcode.cn/problems/combination-sum-iii/
思路与前面的 39,40 大同小异,主要关注递归出口,注意要刚好 k 个。
var res [][]int
func combinationSum3(k int, n int) [][]int {
res = make([][]int, 0)
var tmp []int
help(1, k, n, tmp)
return res
}
// start 开始尝试的数
func help(start, k, n int, tmp []int) {
// 递归出口1:没找到
if n < 0 {
return
}
// 递归出口2:n 为 0
if n == 0 {
// 刚好 k 个
if len(tmp) == k {
tmp1 := make([]int, len(tmp))
copy(tmp1, tmp)
res = append(res, tmp1)
return
}
// 凑不够 k 个
return
}
// 递归出口3:超数了,没找着
if len(tmp) >= k {
return
}
for i:=start; i<=9;i++ {
tmp = append(tmp, i)
help(i+1,k,n-i,tmp)
tmp = tmp[:len(tmp)-1]
}
}
# Leetcode 78 Subsets
https://leetcode.cn/problems/subsets/
求子集,就不需要在递归出口处再将结果保存起来了,每一次尝试,当前的 tmp 都是一个子集。另外,要注意加上空集!
var res [][]int
func subsets(nums []int) [][]int {
res = make([][]int, 0)
var tmp []int
// 空集也是子集之一
res = append(res, tmp)
help(nums, 0, tmp)
return res
}
// start: 从 nums[start] 开始尝试寻找子集
func help(nums []int, start int, tmp []int) {
// 直接保存当前 tmp,因为它就是子集
// 然后再尝试其他的
if len(tmp) > 0 {
tmp1 := make([]int, len(tmp))
copy(tmp1, tmp)
res = append(res, tmp1)
}
// 递归出口
if start == len(nums) {
return
}
for i:=start; i<len(nums); i++ {
tmp = append(tmp, nums[i])
help(nums, i+1, tmp)
tmp = tmp[:len(tmp)-1]
}
}
# Leetcode 401 Binary Watch
https://leetcode.cn/problems/binary-watch/
本题的思路也很简单,就是用回溯,尝试每一种符合条件的开灯情况,hour < 12 && min < 60,递归出口就是刚好开足够 turnedOn 个灯。
var res []string
var values []int
func readBinaryWatch(turnedOn int) []string {
res = make([]string, 0)
values = []int{8,4,2,1,32,16,8,4,2,1}
help(0, turnedOn, 0, 0)
return res
}
// start: 开始扫描 values 的下标
// left: 还有多少个灯没尝试
// hour: 小时
// min: 分钟
func help(start, left, hour, min int) {
// 递归出口1:尝试完 turnedOn 个灯了
if left == 0 {
hs := strconv.Itoa(hour)
ms := ""
if min >= 0 && min < 10 {
ms = "0" + strconv.Itoa(min)
} else {
ms = strconv.Itoa(min)
}
res = append(res, hs + ":" + ms)
return
}
// 递归出口2:start 已经超过 values 的范围了
if left < 0 || start >= len(values) {
return
}
for i:=start; i<len(values); i++ {
v := values[i]
if i <= 3 {
// 小时
if v + hour < 12 {
help(i+1, left-1, v + hour, min)
}
} else {
// 分钟
if v + min < 60 {
help(i+1, left-1, hour, min + v)
}
}
}
}
# 二维平面
二维平面的回溯,常见做法:
- 定义一个变量
directs来保存上下左右四个方向; - 尝试所有起点;
- 四个方向不断尝试;
- 回溯;
- 直到找到结果或者尝试完所有情况。
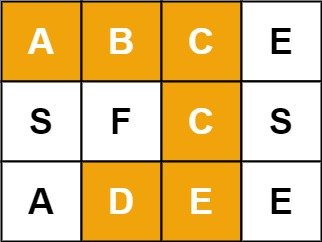
# Leetcode 79 Word Search
https://leetcode.cn/problems/word-search/
思路如上面总结的一样。
var visited [][]bool
var directs = [][]int{
{1,0}, // 左移
{0,1}, // 下移
{-1,0}, // 右移
{0,-1}, // 上移
}
func exist(board [][]byte, word string) bool {
if len(board) == 0 {
return false
}
// 一维是 j
// 二维是 i
// 初始化记录表
visited = make([][]bool, len(board))
for i:=0; i<len(visited); i++ {
visited[i] = make([]bool, len(board[0]))
}
// 尝试每一个起点
for j:=0;j<len(board);j++{
for i:=0;i<len(board[0]);i++ {
if board[j][i] != word[0] {
continue
}
visited[j][i] = true
if help(board, i, j, string(board[j][i]), word) {
return true
}
visited[j][i] = false
}
}
return false
}
// i: 开始尝试的横坐标
// j: 开始尝试的纵坐标
// 本题定义 [i,j] 已经在 tmp 中了
// tmp: 中间结果
func help(board [][]byte, i, j int, tmp, word string) bool {
// 递归出口1:找到了
if tmp == word {
return true
}
// 继续往四个方向尝试
for k:=0;k<len(directs);k++ {
direct := directs[k]
newI := i + direct[0]
newJ := j + direct[1]
if newI < 0 || newI >= len(board[0]) {
continue
}
if newJ < 0 || newJ >= len(board) {
continue
}
if !visited[newJ][newI] && board[newJ][newI] == word[len(tmp)] {
// 尝试
visited[newJ][newI] = true
if help(board, newI, newJ, tmp + string(board[newJ][newI]), word) {
// 找着了直接返回
return true
}
// 没找着就继续尝试,回溯
visited[newJ][newI] = false
}
}
return false
}
# Leetcode 200 Number of Islands
https://leetcode.cn/problems/number-of-islands/
思路:
- 每寻找到一个没访问过的
1,就以它为起点,就把它能连接到的1全部访问一遍;(其实就是 DFS) - 这样遍历完 grid,就知道有多少个 island 了。
var res int
var directs = [][]int{
{1, 0},
{0, 1},
{-1, 0},
{0, -1},
}
var visited [][]bool
func numIslands(grid [][]byte) int {
if len(grid) == 0 {
return 0
}
res = 0
// 初始化访问表
visited = make([][]bool, len(grid))
for i:=0;i<len(grid);i++ {
visited[i] = make([]bool, len(grid[0]))
}
// 寻找 '1',并尝试找其所在的岛屿
for j:=0; j<len(grid);j++ {
for i:=0; i<len(grid[0]); i++ {
if grid[j][i] == '1' && !visited[j][i] {
visited[j][i] = true
help(grid, i, j)
// 当前岛屿已经遍历完了,加1,然后尝试找下一个岛屿
res ++
}
}
}
return res
}
// 将跟 [i,j] 相连的的 '1' 的 visited 全部置为 true
// 其实就是 DFS
func help(grid [][]byte, i, j int) {
for k:=0;k<len(directs);k++ {
direct := directs[k]
newI := i + direct[0]
newJ := j + direct[1]
if newI >= 0 && newI < len(grid[0]) &&
newJ >= 0 && newJ < len(grid) &&
!visited[newJ][newI] && grid[newJ][newI] == '1'{
visited[newJ][newI] = true
help(grid, newI, newJ)
}
}
}
# Leetcode 130 Surrounded Regions
https://leetcode.cn/problems/surrounded-regions/
被围绕的区间不会存在于边界上,换句话说,任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上,或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻,则称它们是“相连”的。
本题可以使用逆向思维:
- 从边缘的
O出发,将它能连接到的O全部标记位 visited; - DFS 所有边缘的
O后,剩下的 !visited,要么就是X,要么就是被X包围的O
var visited [][]bool
var directs = [][]int {
{1, 0},
{0, 1},
{-1, 0},
{0, -1},
}
func solve(board [][]byte) {
if len(board) == 0 {
return
}
// 初始化 visited
visited = make([][]bool, len(board))
for i:=0;i<len(board);i++{
visited[i] = make([]bool, len(board[0]))
}
// 从边缘的 O 出发
for j:=0; j<len(board);j++ {
for i:=0; i<len(board[0]);i++ {
if j == 0 || j == (len(board) - 1) {
if board[j][i] == 'O' && !visited[j][i] {
visited[j][i] = true
dfs(board, i, j)
}
} else {
if i == 0 || i == (len(board[0]) - 1){
if board[j][i] == 'O' && !visited[j][i] {
visited[j][i] = true
dfs(board, i, j)
}
}
}
}
}
// 现在所有没访问过的,就是 X 和被 X 包围的 O
for j:=0;j<len(visited);j++ {
for i:=0; i<len(visited[0]);i++ {
if !visited[j][i] {
board[j][i] = 'X'
}
}
}
}
// 从边缘的 `O` 出发,将所有能连接到的 `O` 全部访问
func dfs(board [][]byte, i, j int) {
for k:=0;k<len(directs);k++ {
direct := directs[k]
newI := i + direct[0]
newJ := j + direct[1]
if newI >= 0 && newJ >= 0 &&
newI < len(board[0]) && newJ < len(board) &&
board[newJ][newI] == 'O' && !visited[newJ][newI] {
visited[newJ][newI] = true
dfs(board, newI, newJ)
}
}
}
# Leetcode 417 Pacific Atlantic Water Flow
https://leetcode.cn/problems/pacific-atlantic-water-flow/
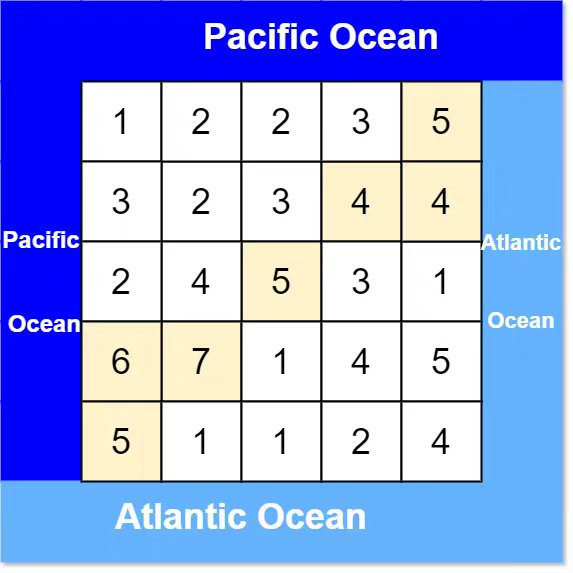
本题核心意思:水只能从高处往低处流,找既能流到大西洋也能流到太平洋的坐标。
思路:逆向思维
- 从太平洋边界出发,逆流而上,看看哪些点可以到太平洋;
- 从大西洋边界出发,逆流而上,看看哪些点可以到大西洋;
- 取交集,便是答案。
var res [][]int
var directs = [][]int {
{1,0},
{0,1},
{-1,0},
{0,-1},
}
var visited1 [][]bool // 太平洋
var can1 [][]bool // 能到太平洋的
var visited2 [][]bool // 大西洋
var can2 [][]bool // 能到大西洋的
func pacificAtlantic(heights [][]int) [][]int {
res = make([][]int, 0)
// 初始化
visited1 = make([][]bool, len(heights))
visited2 = make([][]bool, len(heights))
can1 = make([][]bool, len(heights))
can2 = make([][]bool, len(heights))
for i:=0;i<len(heights);i++ {
visited1[i] = make([]bool, len(heights[0]))
visited2[i] = make([]bool, len(heights[0]))
can1[i] = make([]bool, len(heights[0]))
can2[i] = make([]bool, len(heights[0]))
}
// 上边界
for p:=0;p<len(heights[0]);p++ {
can1[0][p] = true
visited1[0][p] = true
pacific(heights, p, 0)
}
// 左边界
for p:=1;p<len(heights);p++ {
can1[p][0] = true
visited1[p][0] = true
pacific(heights, 0, p)
}
// 下边界
for p:=0;p<len(heights[0]);p++ {
can2[len(heights)-1][p] = true
visited2[len(heights)-1][p] = true
atlantic(heights, p, len(heights)-1)
}
// 右边界
for p:=0;p<len(heights)-1;p++ {
can2[p][len(heights[0])-1] = true
visited2[p][len(heights[0])-1] = true
atlantic(heights, len(heights[0])-1, p)
}
// 取交集
for j:=0; j<len(heights); j++ {
for i:=0; i<len(heights[0]); i++ {
if can1[j][i] && can2[j][i] {
res = append(res, []int{j, i})
}
}
}
return res
}
// 逆流而上,看看哪些能流到太平洋
func pacific(heights [][]int, i, j int) {
// 向四个方向走
for k:=0;k<len(directs);k++{
direct := directs[k]
newI := i + direct[0]
newJ := j + direct[1]
if newI >= 0 && newI < len(heights[0]) &&
newJ >=0 && newJ < len(heights) && !visited1[newJ][newI]{
// 逆流而上
if heights[newJ][newI] >= heights[j][i] {
visited1[newJ][newI] = true
can1[newJ][newI] = true
pacific(heights, newI, newJ)
}
}
}
}
// 逆流而上,看看哪些能流到大西洋
func atlantic(heights [][]int, i, j int) {
// 向四个方向走
for k:=0;k<len(directs);k++{
direct := directs[k]
newI := i + direct[0]
newJ := j + direct[1]
if newI >= 0 && newI < len(heights[0]) &&
newJ >=0 && newJ < len(heights) && !visited2[newJ][newI]{
// 逆流而上
if heights[newJ][newI] >= heights[j][i] {
visited2[newJ][newI] = true
can2[newJ][newI] = true
atlantic(heights, newI, newJ)
}
}
}
}
# Leetcode 51 N Queens
https://leetcode.cn/problems/n-queens/
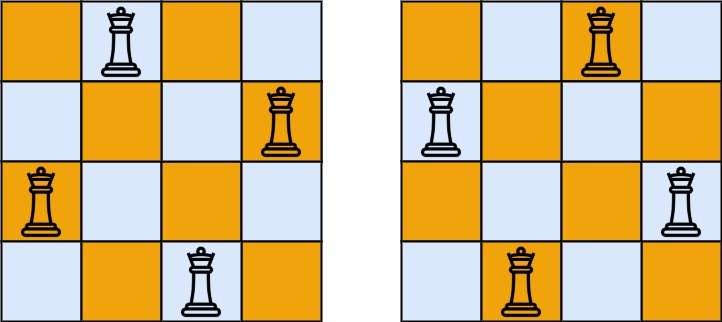
核心点是如何快速判断不合法的情况:
col[i] 表示第 i 列已经被占用。
dia1[k] 表示从左下到右上的对角线已经被占用,观察左下到右上的对角线会发现有特点:
j+i为定值,且有 2n-1 个对角线。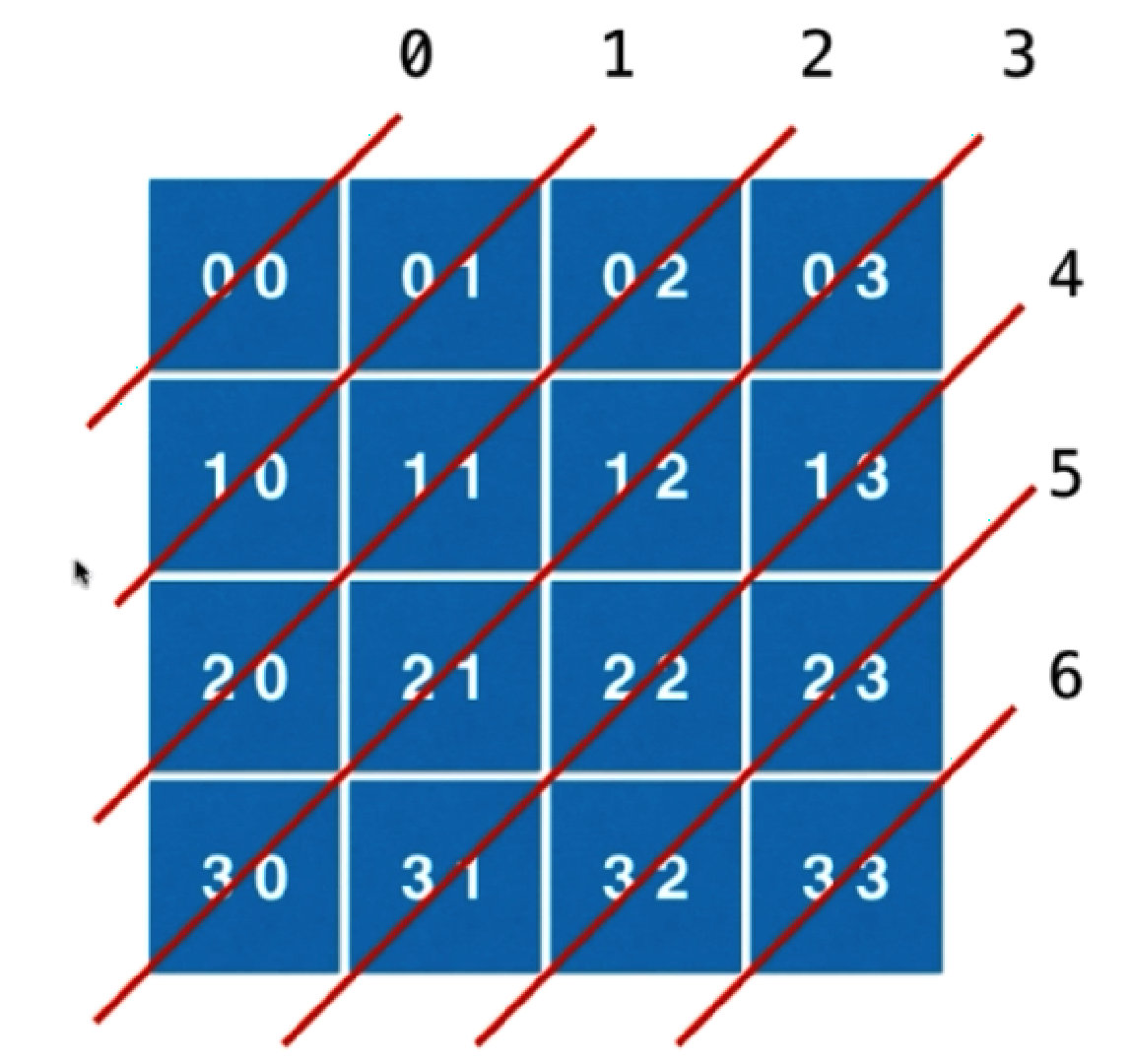
dia2[k] 表示从左上到右下的对角线已经被占用,观察左上到右下对角线会发现有特点:i-j 为定值,且有 2n-1 个对角线,如果转为非负数,那便是
j-i+n-1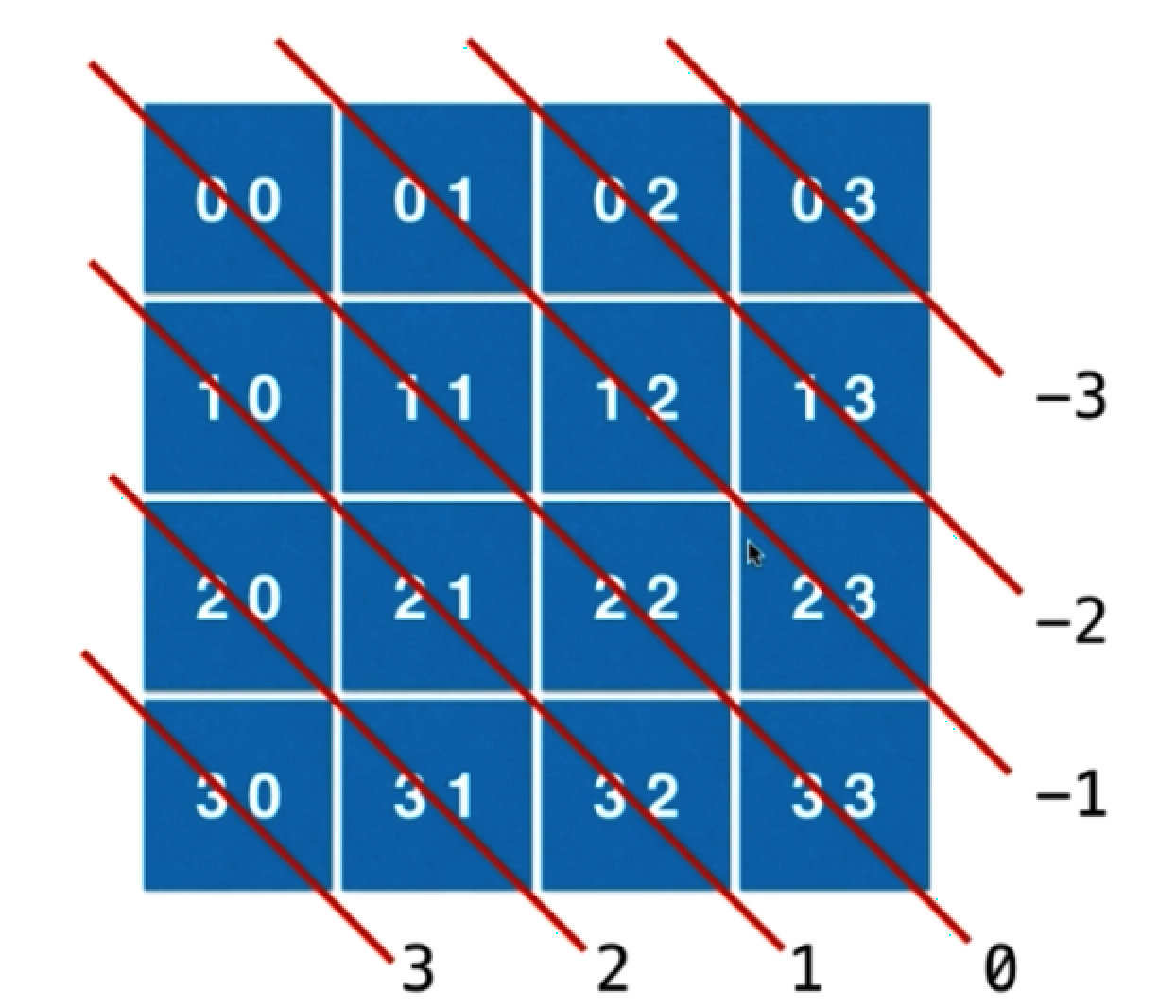
var col []bool // 第 i 列已经被占用了
var dia1 []bool // 第 i 个左下到右上对角线已经被占用
var dia2 []bool // 第 i 个左上到右下对角线已经被占用
var res [][]string
func solveNQueens(n int) [][]string {
if n == 0 {
return nil
}
col = make([]bool, n)
dia1 = make([]bool, 2 * n - 1)
dia2 = make([]bool, 2 * n - 1)
res = make([][]string, 0)
var tmp []int
help(n, 0, tmp)
return res
}
// curLine: 尝试第几行
func help(n int, curLine int, tmp []int) {
// 递归出口,n 个皇后都已经置放完毕
if curLine == n {
res = append(res, build(tmp))
return
}
// 尝试当前行的每一种可能
for i:=0;i<n;i++ {
if canUse(i, curLine, n) {
// 尝试
col[i] = true
dia1[curLine+i] = true
dia2[curLine-i+n-1] = true
tmp = append(tmp, i)
// 递归尝试
help(n, curLine + 1, tmp)
// 回溯
col[i] = false
dia1[curLine+i] = false
dia2[curLine-i+n-1] = false
tmp = tmp[:len(tmp)-1]
}
}
}
// 将一个 tmp 转为 n 皇后结果
func build(tmp []int) []string {
res := make([]string, 0, len(tmp))
for i:=0;i<len(tmp);i++ {
s := ""
val := tmp[i]
for j:=0;j<val;j++ {
s += "."
}
s += "Q"
for j:=val+1;j<len(tmp);j++ {
s += "."
}
res = append(res, s)
}
return res
}
// 判断该位置是否可用
func canUse(i, j, n int) bool {
return !col[i] && !dia1[j+i] && !dia2[j-i+n-1]
}
# Leetcode 52 N Queens II
https://leetcode.cn/problems/n-queens-ii/
本题跟上一题思路完全一致,只是不需要生成棋盘,只需要记录个数即可。
var col []bool // col[i] 已经被占用了
var dia1 []bool // 左下到右上对角线 dia1[k] 已经被占用了
var dia2 []bool // 左上到右下对角线 dia2[k] 已经被占用了
var res int
func totalNQueens(n int) int {
col = make([]bool, n)
dia1 = make([]bool, 2*n-1)
dia2 = make([]bool, 2*n-1)
res = 0
help(n, 0)
return res
}
// start 表示要尝试第几个皇后,从 0 开始
func help(n, start int) {
if start == n {
res ++
}
// 每一行,尝试每一列
for i:=0;i<n;i++ {
if canUse(i, start, n) {
col[i] = true
dia1[start + i] = true
dia2[start - i + n - 1] = true
help(n, start + 1)
col[i] = false
dia1[start + i] = false
dia2[start - i + n - 1] = false
}
}
}
// 判断 [i,j] 是否可以置放皇后
func canUse(i, j, n int) bool {
return !col[i] && !dia1[j+i] && !dia2[j-i+n-1]
}
